Tvorba jednoduché scény
V každodenní praxi učitele se mohou vyskytnout situace, kdy potřebuje improvizovat. Vytvoření experimentu v průběhu hodiny může být náročné. Algodoo je na tuto situaci velmi vhodné. Lze v něm vytvořit funkční simulaci za 1-5 minut.
Ukažme si takovou situaci:
7. ročník
Učivo o otáčivém pohybu
Tato scéna vychází z reálné situace, kdy žáci nedokázali popsat vlastnosti otáčivého pohybu a nedokázali popsat rozdíl mezi otáčivým a posuvným pohybem. Rychle vytvořená simulace v Algodoo byla velmi názorná a pomohla žákům poznat a popsat rozdíl.
Předpoklady
Žáci viděli několik těles, která se otáčejí - kolo u automobilu, vodní kolo, houpačka.
Žáci vyzkoušeli otáčivý pohyb pomocí "káči" a rozhoupáním závaží zavěšeného na provázku.
Cíle simulace
Žáci odvodí:
Trajektorie libovolného bodu tělesa otáčejícího se okolo osy tvoří kružnici (nebo její část) se středem v ose otáčení.
Čím je tento bod dál od osy, tím se pohybuje rychleji.
Žáci popíší rozdíly mezi posuvným a otáčivým pohybem.
Tvorba simulace
Otevřeme novou scénu a odstraníme rovinu, tíhovou sílu i tření vzduchu.
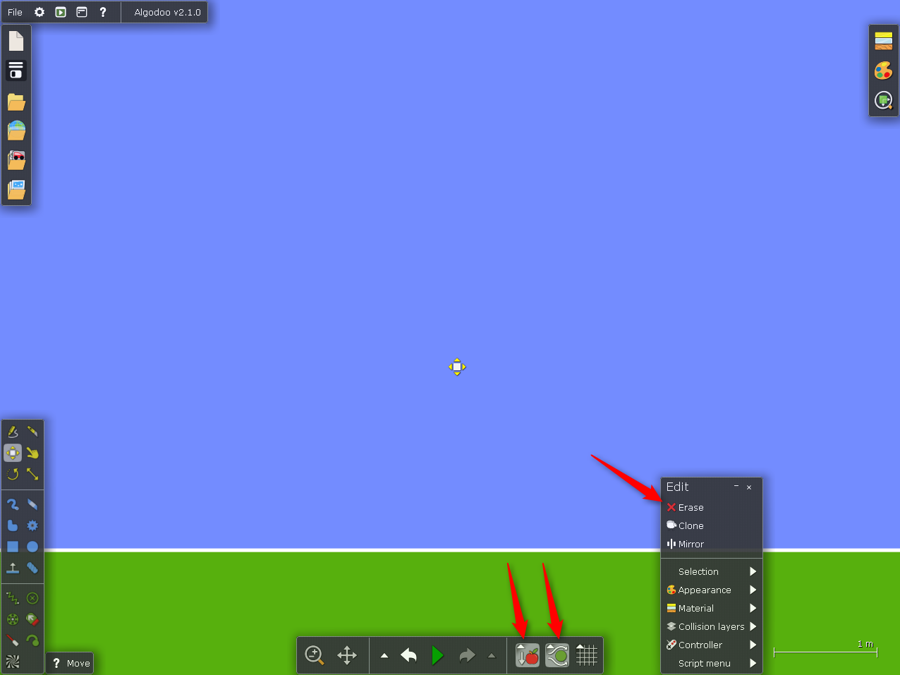
Vytvoříme kruh a pomocí kontextové nabídky vložíme hřídel.
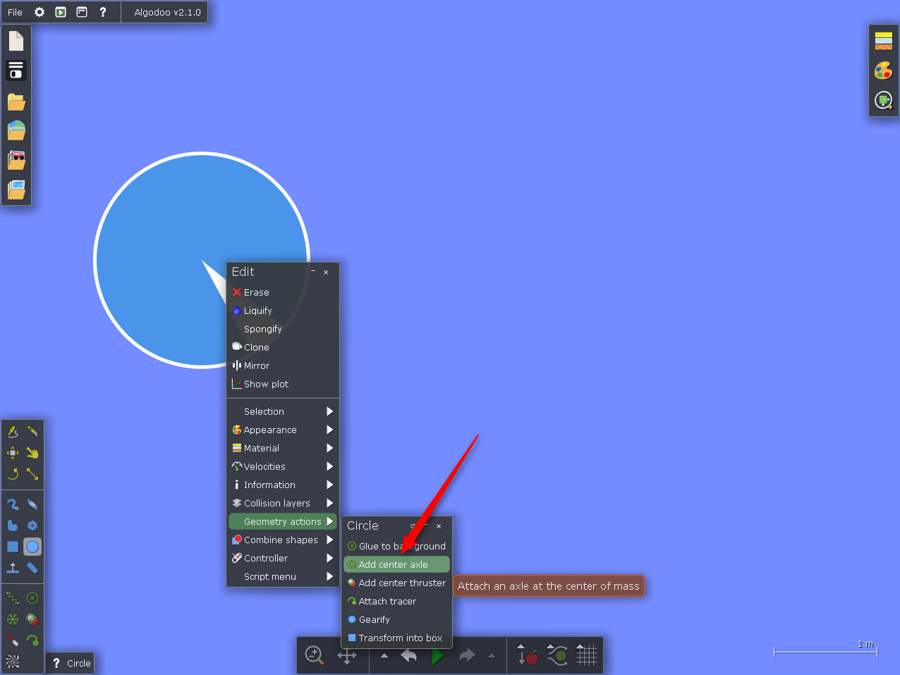
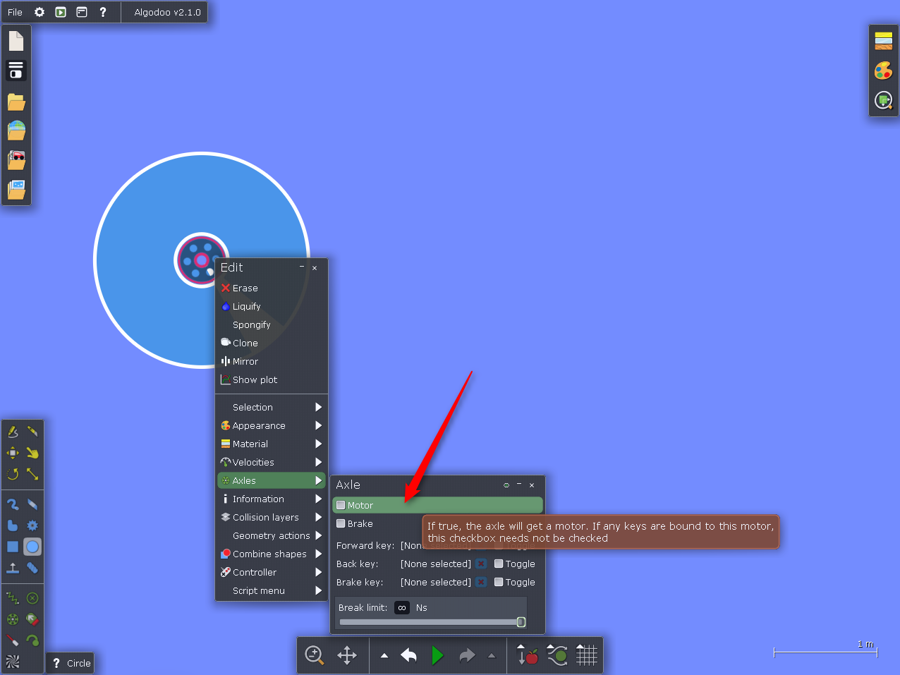
K hřídeli připojíme motor.
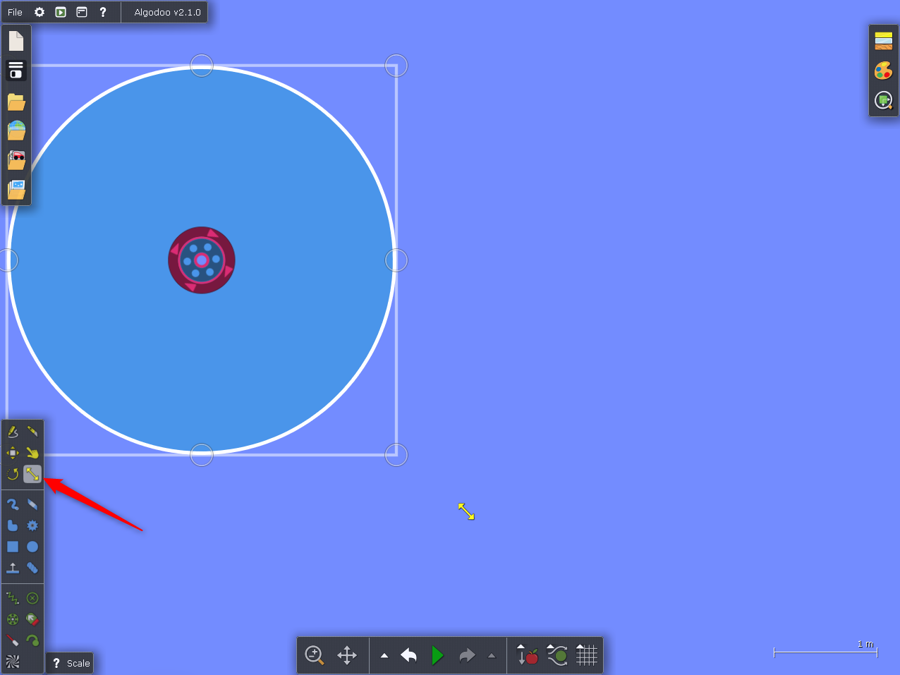
Podle potřeby zvětšíme kruh pomocí nástroje Scale tool (podržením tlačítka Shift zachováme poměr stran).
Vložíme 2x stopu pomocí Tracer tool. Nic dalšího nenastavujeme. Implicitní hodnoty jsou dostatečně názorné.
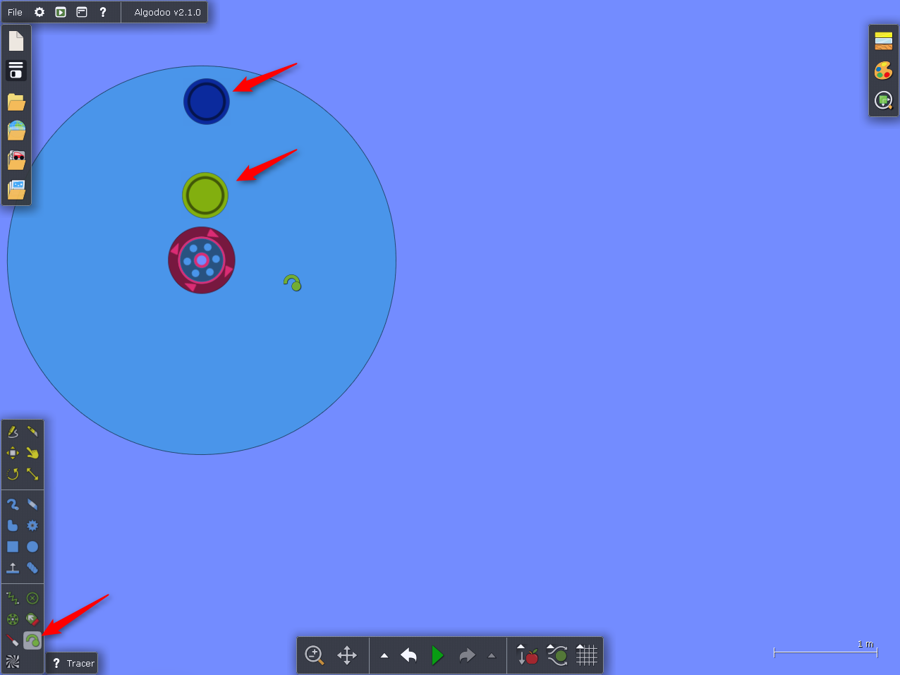
Máme nachystanou scénu pro otáčivý pohyb. Můžeme ji použít samostatně nebo doplnit o část s posuvným pohybem.
Vytvoříme menší objekt jakéhokoliv tvaru a nastavíme jeho rychlost a směr pomocí kontextové nabídky.

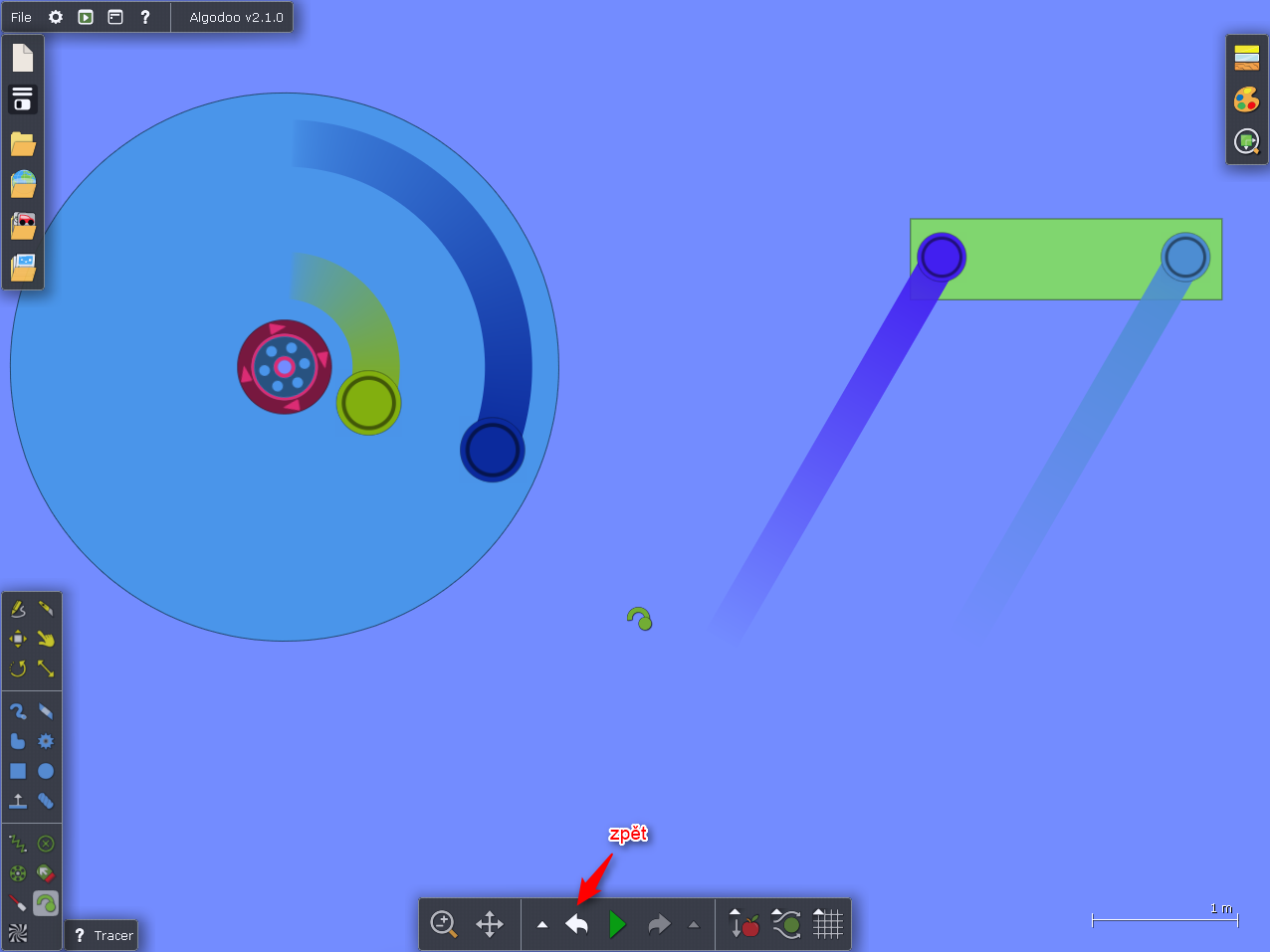
Připojíme stopy jako v předchozím případě. Můžeme scénu spustit pomocí mezerníku a sledujeme chování stop. Stopy jsou nastavené tak, že po daném čase mizí (implicitně je nastaveno pro všechny 1,5 s). Bod, který za sebou zanechá delší stopu je rychlejší. Lze sledovat tvar stopy.
Poznámka: Pokud se chceme vrátit na začátek simulace, protože obdélníkový objekt nám "uteče" mimo obraz, stačí zmáčknout tlačítko Zpět.
Scéna je ke stažení ZDE.
Žáci odvodí vlastnosti trajektorií otáčivého a posuvného pohybu a mohou si simulaci zakreslit do sešitu tak, jak ji vidí na posledním obrázku.
Last updated